Les Automated Market Makers à fonction constante – Les AMM décodés

Comme nous l’avons vu cette série consacrée aux AMM (automated market makers ou faiseurs de marché automatisés), les premiers algorithmes concernaient les marchés prédictifs. C’est le cas du modèle LMSR, repris sur Ethereum par Gnosis et Augur. Il existe d’autres modèles pour les marchés où l’agrégation d’informations est très importante, et où les profits dépendant de la capacité à évaluer les probabilités de la survenue d’événements futurs.

Bancor fut le premier AMM on-chain pour la finance décentralisée (DeFi). Sa fonction de prix spécifie le cours d’un actif en se basant sur sa quantité totale disponible : la bonding curve. Le prix d’équilibre résultant de cette courbe de liaison équivaut au prix du marché sous certaines conditions.

Un AMM agrège de la liquidité pour une place de marché numérique, de façon décentralisée et sans permission. Il y a plusieurs façons de définir les dynamiques entre les réserves de chaque actif (liquidity pools).

Les AMM peuvent utiliser diverses fonctions pour définir ces relations entre les réserves de liquidité. Dans la finance décentralisée, il existe un modèle largement employé. Il est appelé Constant Function Market Maker (CFMM) – faiseur de marché à fonction constante.

L’équipe de développement d’Uniswap l’implémenta pour la première fois en 2019. Le modèle à produit constant est le point de départ d’une nouvelle génération d’AMM.

Table des matières

• Les AMM à fonction constante (CFMM)
  • La formule du produit constant
  • Intérêt
  • Bénéfices
• Formalisation du modèle d’AMM à produit constant
  • Modification des réserves de jetons
  • Incidence des frais
• Fonctions de l’AMM à produit constant
  • Fonctions de liquidité
  • Apporter de la liquidité ( liquidity minting )
  • Retirer de la liquidité (burning liquidity)
  • Mécanisme de pricing de l’AMM à fonction constante
  • Apport en liquidité
  • Homogénéité des modèles d’AMM en cas de réserves de liquidité uniformes
  • Impact d’un trade sur le prix et slippage
  • Fonctions d’échange de jetons
• Implémentation des AMM à fonction constante
• Bibliographie

Les AMM à fonction constante (CFMM)

Comme nous les avons décrits brièvement dans la seconde partie de cette série, les CFMM sont conçus pour garder le produit des réserves de liquidité allouées au marché constant. Par exemple, il peut s’agir d’un pool d’ethers (ETH), et du pool correspondant d’un jeton ERC-20 spécifique.

N’importe quel échange (trade) affecte les pools de liquidité du marché. Il entraîne l’ajout de fonds d’un côté, et le retrait de liquidités de l’autre.

Les plateformes d’échange décentralisées (DEX) utilisant des AMM comprennent 3 types de participants :

• Traders : les utilisateurs souhaitant vendre, acheter ou échanger des jetons ;
• Fournisseurs de liquidité (liquidity providers ou LP) : ces utilisateurs souhaitent générer un profit en ajoutant des liquidités dans les pools du marché ;
• Arbitrageurs : ce sont des traders, qui vont générer du profit en exploitant les fluctuations du prix d’un actif au sein d’un AMM. Lorsque le cours d’un actif sur le DEX diverge de son prix sur d’autres exchanges, ils saisissent cette opportunité.

Les AMM à fonction constante se basent sur une formule mathématique très simple pour définir la relation entre les réserves de deux actifs financiers. Ces deux actifs composent les deux côtés d’une paire de trading.

La formule du produit constant

Un automated marker maker à produit constant satisfait l’équation suivante :

(RX – Δx) x (RY + γΔy) = k

Où :

• RX est la quantité de l’actif X en réserve ;
• RY est la quantité de l’actif Y en réserve ;
• Δx est la quantité d’actif X acheté ;
• γ est la commission (les frais) pour la transaction.

Avec cette fonction, pour n’importe quelle quantité d’actif X ou Y échangée, les réserves en sont affectées de telle sorte que, sans frais de transaction, le produit RX x RY reste égal à la constante k.

La version simplifiée de cette formule est donc :

x * y = k

Où x et y représentent les réserves de chaque actif. Lorsque les frais de trading sont ajoutés aux réserves (ce qui est le cas avec le protocole Uniswap par exemple) chaque trade augmente graduellement k.

Le graphe de la fonction forme ainsi une hyperbole, lorsqu’on place les quantités des deux actifs sur leurs axes respectifs x et y.

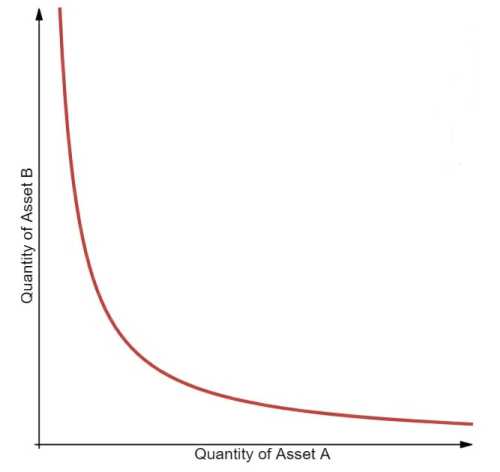
La propriété désirée est donc d’avoir toujours de la liquidité disponible, même si les prix tendent vers l’infini.

Le prix p de l’actif est dérivé de la relation entre les soldes des deux réserves (le liquidity pool de chaque token). On le définit ainsi :

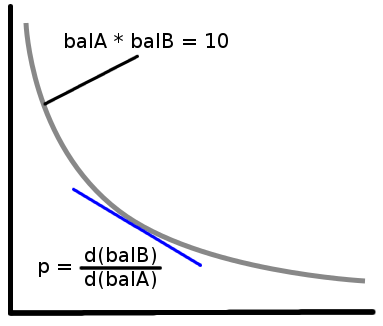
balA/balB : solde (balance) de l’actif A/B.

Ici, p est donc le prix du jeton B (Y), libellé en jeton A (X).

Intérêt

Ce modèle empêche l’AMM de tomber à court de liquidité, que ce soit par excès de demande, ou dans le cas où un attaquant souhaiterait drainer les liquidity pools – cette attaque est appelée money pumping. Lors d’un échange, plus la quantité achetée est grande, et plus le taux d’échange marginal devient élevé pour chaque unité additionnelle.

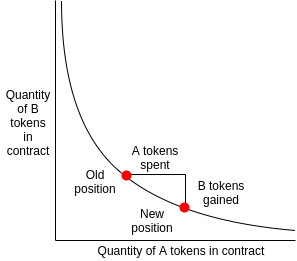
Évolution des réserves dans le cas du produit constant – Extrait du whitepaper de Curve Finance.

Le market maker génère du profit en ajoutant des frais de transaction (0,3 % pour Uniswap, par exemple).

Bénéfices

Le modèle d’AMM à produit constant va plus loin que les précédents et offre plusieurs avantages.

Des échanges plus rapides

Avec un système de carnet d’ordres, le market making, et l’exécution des trades en général, requièrent plusieurs étapes. Les market makers doivent tout d’abord créer leurs ordres, puis les publier dans le carnet de l’exchange. Ensuite, les traders vont remplir les ordres qui les intéressent. Les markets makers devront donc attendre que leurs ordres soient exécutés.

Avec un AMM à produit constant, les trades sont exécutés directement on-chain, sans intermédiaire. Le délai d’exécution dépend des capacités de la blockchain. La fonction constante assure qu’il y aura toujours de la liquidité disponible.

Amorçage de la liquidité

Apporter de la liquidité sur une plateforme d’échange centralisée, traditionnelle, est un processus long et coûteux. Premièrement, les plateformes doivent attirer des market makers – généralement en leur fournissant des fonds, et des trading desks personnalisés. Deuxièmement, les market makers doivent créer les algorithmes qui vont distribuer la liquidité à travers le carnet d’ordres. Enfin, ces derniers, qui doivent constamment se couvrir contre le risque (hedging) vont jouer un rôle actif, et utiliser plusieurs plateformes différentes.

Avec les AMM à fonction constante, les fournisseurs de liquidité jouent un rôle beaucoup plus passif. Ils vont seulement déposer leurs fonds sur les coffres de l’exchange (les liquidity pools) et attendre que les trades aient lieu. Plusieurs mécanismes d’incitation économique assurent que les market makers pourront profiter de l’immobilisation de leurs actifs dès le lancement du marché. De cette façon, la liquidité est disponible rapidement pour tous les participants.

L’indépendance des chemins

La découverte du prix d’un actif est dite path-dependant lorsqu’elle est influencée par le comportement des participants au marché. C’est le cas pour les exchanges centralisés, où les prix sont affectés par la profondeur du marché, l’historique des échanges, ou d’autres informations qui ne sont disponibles que pour certains participants.

Avec un AMM à fonction constante, la découverte du prix est path-independant. En effet, la fonction de prix ne prend en compte que les quantités disponibles de chaque actif et non le chemin que les liquidités ont emprunté entre elles. Ainsi, l’état du marché n’est défini que par ce paramètre – la quantité d’actifs en réserve.

Les oracles on-chain

Sous les bonnes conditions, les AMM peuvent fournir des oracles de prix on-chain pour les actifs déposés dans les pools de liquidité. Pusiqu’il y a des opportunités d’arbitrage, lorsque le prix d’un actif au sein de l’AMM diverge de son prix sur des exchanges externe, on peut assumer que le prix de l’AMM reflétera le prix global du marché.

C’est vrai en théorie, mais en pratique, il faut être certain que personne ne peut manipuler le prix donné par l’oracle.

Formalisation du modèle d’AMM à produit constant

Dans cette partie, nous allons faire un peu de mathématiques et décrire la formalisation du pricing d’un jeton lors d’un échange.

Soient deux réserves de jetons. Considérons un DEX qui permet d’échanger deux jetons, X et Y.

• Soit x le nombre de jetons X en réserve ;
• Soit y le nombre de jetons Y en réserve.

Le prix d’échange du jeton (token exchange price) est déterminé par le ratio entre x et y – de telle façon que le produit x x y reste constant.

• Soit ∆x la quantité de jetons X vendus ;
• Soit ∆y la quantité de jetons Y correspondante.

La relation entre ∆x, ∆y et le produit x x y est donc la suivante :

x x y = (x + ∆x) x (y – ∆y)

Notre prix d’échange (∆x/∆y) est donc fonction de x/y.

Modification des réserves de jetons

Après l’échange, les réserves sont alors mises à jour comme suit :

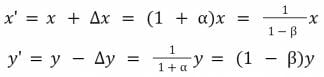
Où :

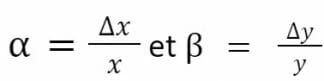
De la même façon :

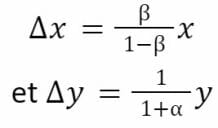
Incidence des frais

Soient ρ les frais prélevés pour chaque échange de jetons. Nous avons donc 0 ≤ ρ < 1 avec ρ = 0,003 pour des frais standard de 0,3 %. Soit γ = 1 – ρ. Désormais :

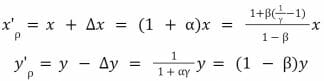
Où :

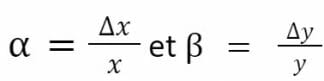
Nous avons aussi :

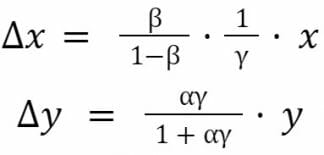
Si nous n’avons aucun frais pour l’échange, alors γ = 1. Lorsque γ < 1, le produit x x y va augmenter lors de chaque trade :

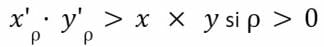
Le produit reste constant lorsqu’il n’y a pas de frais :

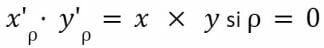
Fonctions de l’AMM à produit constant

Avec ce modèle, soit X le jeton représentant l’ether (ETH) et Y le jeton ERC-20 correspondant pour l’échange effectué. Nous avons différentes fonctions au sein du protocole.

Fonctions de liquidité

Le protocole utilise les fonctions suivantes pour créer (to mint) et détruire (to burn) les jetons permettant de garder la trace des liquidités déposées et retirées par chaque compte Ethereum. On appelle ces jetons Liquidity Provider tokens (LP tokens) ou Exchange tokens.

• addLiquidity

Cette fonction crée (mint) les LP tokens correspondant à la liquidité apportée dans le pool.

• removeLiquidity

Cette fonction brûle (burn) les LP tokens correspondant à la liquidité retirée du pool.

Ces deux fonctions sont l’implémentation des formules mathématiques décrite plus haut, en utilisant l’arithmétique entière. Cela permet ainsi d’éviter les erreurs d’approximation dues aux arrondis entiers, qui pourraient être exploitées par l’utilisateur pour faire de l’argent “gratuit”.

Apporter de la liquidité (liquidity minting)

Lorsque de la liquidité est apportée en ether (jeton X), le fournisseur “crée” de la liquidité. La définition mathématique du procédé est alors la suivante :

Soit (e, t, l) le tuple représentant l’état de l’AMM, où :

• e est la quantité d’ETH en wei ;
• t est le nombre de LP tokens ;
• l est la quantité totale de liquidité.

La fonction addLiquidity accepte alors en entrée ∆e > 0 et met à jour l’état de l’AMM comme suit.

• Le tuple (e, t, l) devient (e’, t’, l’) où :

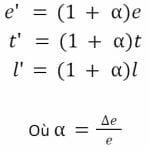
Ainsi, un fournisseur de liquidité ajoutant ∆e wei et ∆t = t’ – t jetons ERC-20 dans les réserves va créer (mint) ∆l = l’ – l liquidité.

Le ratio entre e, t et l est préservé. Le produit k = e x t augmente.

En effet, soit (e, t, l) → addLiquidity (e’, t’, l’) le changement d’état de l’AMM. Soient k = e x t et k’ = e’ x t’. Alors :

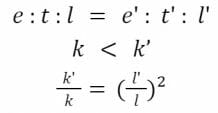
Avant de passer à la fonction opposée (retrait de liquidité), il nous faut mentionner l’arrondi.

Arrondi entier

Pour une implémentation utilisant l’arithmétique entière, l’approximation de t’ et de l’ (qui ne sont pas des entiers) est formulée de la manière suivante.

La fonction addLiquidity, une fois codée, reçoit en entrée un entier ∆e > 0 ∈ Z. L’état de l’AMM est mis à jour ainsi :

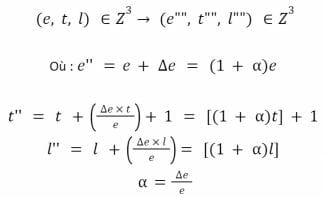
Si nous revenons à notre fonction addLiquidity spécifiée précédemment, nous avons donc les relations suivantes entre les tuples (e, t, l) et (e”, t”, l”) :

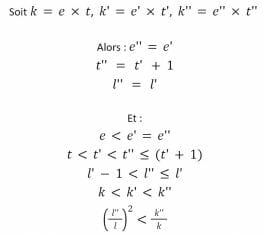
De cette façon, t’ est approximé vers une plus grande valeur t”, mais dans tous les cas :

0 < t” – t’ ≤

Tandis que l’ est approximé vers une plus petite valeur l”, dans tous les cas :

-1 < l” – l’ ≤ 0

Nous obtenons donc la propriété désirée pour le schéma d’approximation :

k” >> k’

Dans la pratique, cela signifie que lorsqu’un fournisseur de liquidité dépose plus de jetons que nécessaire dans la réserve (jusqu’à 1), il va “mint” moins de liquidité que leur valeur mathématique (jusqu’à -1).

Retirer de la liquidité (burning liquidity)

Lorsqu’un liquidity provider souhaite retirer tout ou partie de ses ETH et jetons ERC-20 des pools, il va brûler la liquidité (les LP tokens) correspondante. La fonction est removeLiquidity.

removeLiquidity reçoit en entrée 0 < ∆l < l et l’état de l’AMM est mis à jour ainsi :

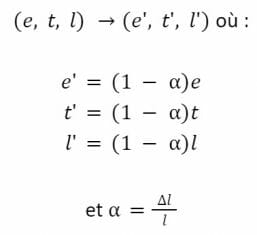
L’utilisateur brûle donc ∆l liquidité tandis qu’il retire ∆e = e – e’ wei et ∆t = t – t’ jetons ERC-20. Il s’agit de la définition mathématique du “burn” de liquidité, qui est duale au “mint” de liquidité, et il en va de même pour l’invariant :

Soient k = e x t et k’ = e’ x t’. Alors :

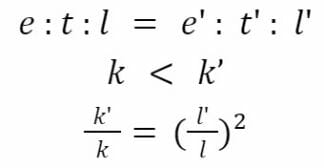
D’autre part, si :

(e0, t0, l0) addLiquidity (∆e) → (e1, t1, l1) removeLiquidity (∆l) → (e2, t2, l2)

Avec ∆l = l1 – l0 alors :

e0 = e2, t0 = t2 et l0 = l2

Pour l’implémentation en arithmétique entière, e’ et t’ doivent être approximés, puisqu’ils ne sont pas entiers. La formulation est conçue de la même façon que pour la fonction addLiquidity.

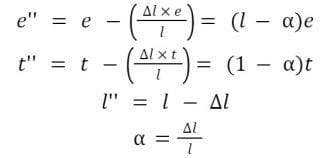
Nous avons bien les propriétés désirées pour k’‘ car :

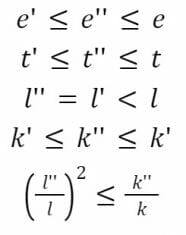
e’ et t’ sont approximés en e” et t”. Cela signifie dans la pratique que lorsqu’un fournisseur de liquidité retire des fonds, il peut se retrouver avec une quantité moindre que la valeur mathématique de son dépôt. Encore une fois, cela permet d’éviter les erreurs d’arrondi.

Mécanisme de pricing de l’AMM à fonction constante

Pour calculer le prix courant d’un jeton, nous disposons de deux fonctions : getInputPrice et getOutputPrice. Il faut encore une fois prendre en compte l’arrondi à l’entier lors de leur implémentation, et faire des ajustements corrects. Ces deux fonctions sont seulement dédiées au pricing des jetons et n’ont donc aucun impact sur l’état de l’AMM.

Prix d’entrée

Cette fonction calcule combien de jetons Y (= ∆y ) peuvent être achetés en vendant une quantité ∆x d’ETH (en wei).

Soient ρ les frais de l’échange de jetons. La fonction getInputPrice reçoit en entrée ∆x > 0, x et y. L’image (en sortie) est ∆y tel que :

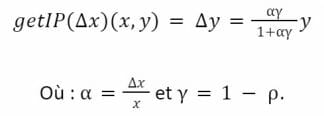
Nous obtenons ainsi les deux relations suivantes :

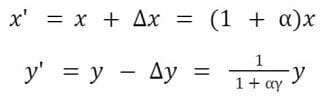
Soient k = x x y et k’ = x’ x y’. Alors : x < x’, y > y’ et k < k’.

Lors de l’implémentation de la fonction, avec des frais de ρ, nous avons x et y ∈ Z (entiers relatifs). Le calcul est alors basé sur une division entière avec troncature.

Si nous supposons que getInputPrice (x’ – x)(x, y) = y’ – y avec k = x x y, k’ = x’ x y’ et k” = x” x y” alors nous avons bien :

• x < x’ = x”
• y’ ≤ y” ≤ y
• k < k’ ≤ k”

Prix de sortie

La fonction getOutputPrice est formalisée comme suit.

Soient ρ les frais de l’échange de jetons. La fonction getOutputPrice reçoit en entrée 0 < ∆y < y et x, x et y. L’image (en sortie) est ∆x tel que :

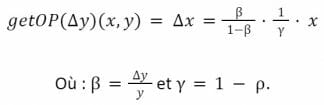
Nous avons alors les relations suivantes :

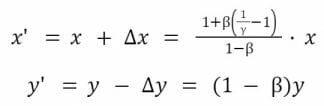
Si nous supposons que getOutputPrice (y’ – y)(x, y) = x’ – x avec k = x x y, k’ = x’ x y’ alors nous avons bien : x < x’, y’ < y et k < k’.

getOutputPrice est donc la fonction duale de getInputPrice :

• getOutputPrice (getInputPrice (∆x)(x, y))(x, y) = ∆x
• getInputPrice (getOutputPrice (∆y)(x, y))(x, y) = ∆y

Tout comme pour la fonction getInputPrice, avec des frais de ρ pour le trade, nous aurons x et y ∈ Z et une division entière avec troncature.

Si nous supposons que getOutputPrice (y’ – y)(x, y) = x’ – x avec k = x x y, k’ = x’ x y’ et k” = x” x y”. Soit k” = tA” * tB”, alors nous avons bien :

• x < x’ < x”
• y’ = y” < y
• k < k’ < k”

Nous allons maintenant examiner les fonctions d’échange de jetons qui permettent de mettre à jour l’état des réserves de l’AMM.

Apport en liquidité

Nous désirons une formule pour l’apport de liquidité (liquidity provisioning) satisfaisant une règle de pricing donnée.

Considérons une paire de trading : jeton X et jeton Y. Soit dx la quantité de jeton X vendue au pool. La réserve RX va augmenter de dx et la réserve RY va baisser de dy.

Le prix auquel le jeton X sera vendu lors du trade peut être défini par le ratio (-dy/dx) – en considérant un dx infinitésimalement petit. Ainsi :

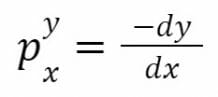
Cette équation nous donne la relation entre le prix du trade, les soldes des réserves de jetons, et le ratio des réserves pour X et Y, aussi bien que l’invariant, en résolvant l’équation différentielle.

Par exemple, dans le cas d’une fonction à somme constante :

Il nous faut trouver une fonction qui donne toujours le prix constant de 1. Nous avons :

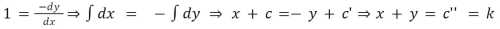
Nous tombons alors sur le modèle de la somme constante : x + y = k.

Autre exemple, dans le cas d’une fonction à produit constant :

Considérons deux pools de liquidité (jetons X et Y) de valeur équivalente (50%/50%). Nous devons trouver une fonction par laquelle le prix de x est seulement basé sur le ratio entre x et y. Nous avons donc :

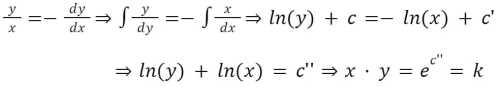
Et nous retrouvons bien la formule du produit constant, x x y = k.

Homogénéité des modèles d’AMM en cas de réserves de liquidité uniformes

Avec les équations relatives aux échanges de jetons mentionnées ci-dessus, nous pouvons prouver que le modèle d’AMM à produit constant et le modèle à somme constante sont les mêmes lorsque les réserves de jeton sont équivalentes, c’est-à-dire lorsque RX = RY.

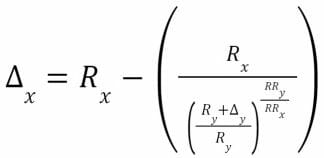
Puisque nous avons RRX = RRY’ alors :

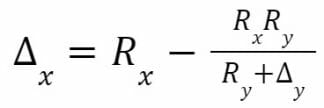
Cela implique donc :

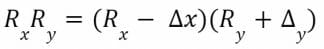
C’est l’équation décrivant le modèle à produit constant. Nous pouvons calculer le prix marginal pour le jeton X (prix d’un trade infinitésimal) en dérivant cette formule :

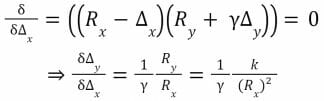
Comme nous l’avons vu précédemment, le prix de x relativement à y forme une hyperbole.

Impact d’un trade sur le prix et slippage

Nous désirons ici quantifier l’impact d’un trade sur le prix d’un jeton donné.

L’impact de l’échange dépend de la courbure de la fonction définissant le prix relatif de deux (ou plusieurs) actifs. Comme nous pouvons l’observer, l’impact de l’échange (qui est également le price sensitivity, la sensibilité du prix) est une fonction continue non-linéaire.

• Soit 0  ≤ f  ≤ 100 ;
• Considérons la vente d’une quantité fRx de x jetons à l’AMM.

Grâce à la dernière équation nous savons que le prix de x avec une réserve Rx avant le trade est :

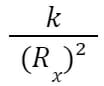
Après le trade, le prix devient :

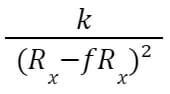
Le pourcentage de variation du prix est alors :

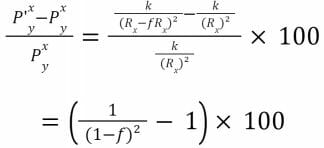
Nous pouvons ainsi observer que le changement du prix, pour une quantité donnée de jetons échangés, est non-linéaire. Cela implique donc du slippage pour les traders : plus le trade est important, plus il y a de slippage quant au prix.

Fonctions d’échange de jetons

Pour mettre à jour l’état de l’AMM lors d’un échange, nous avons trois fonctions principales : ethToToken, tokenToEth and tokenToToken.

ethToToken

La fonction ethToToken reçoit en entrée ∆e avec ∆e > 0 et met à jour l’état de l’AMM de (e, t, l) vers (e’, t’, l) de la façon suivante :

• e’ = e + ∆e
• t’ = t – getInputPrice (∆e, e, t)

Lors de l’implémentation, ∆e est un paramètre entier.

ethToTokenExact

La fonction ethToTokenExact reçoit en entrée ∆t avec 0 < ∆t < t et met à jour l’état de l’AMM de (e, t, l) vers (e’, t’, l) de la façon suivante :

• t’ = t – ∆t
• e’ = e + getOutputPrice (∆t, e, t)

Lors de l’implémentation, ∆t est un paramètre entier.

tokenToEth

La fonction tokenToEth reçoit en entrée ∆t avec ∆t > 0 et met à jour l’état de l’AMM de (e, t, l) vers (e’, t’, l) de la façon suivante :

• t’ = t + ∆t
• e’ = e – getInputPrice (∆t, t, e)

Lors de l’implémentation, ∆t est un paramètre entier.

tokenToEthExact

La fonction tokenToEthExact reçoit en entrée ∆e avec 0 < ∆e < e et met à jour l’état de l’AMM de (e, t, l) vers (e’, t’, l) de la façon suivante :

• e’ = e – ∆e
• t’ = t + getOutputPrice (∆e, t, e)

Lors de l’implémentation, ∆t est un paramètre entier.

tokenToToken

Soient A et B deux smart contracts d’échange pour l’AMM, dont les états sont les tuples suivants :

[(eA, tA, lA), (eB, tB, lB)]

La fonction tokenToToken reçoit en entrée ∆tA avec ∆tA > 0 et met à jour l’état de [(eA, tA, lA), (eB, tB, lB)] vers [(e’A, t’A, lA), (e’B, t’B, lB)] où :

• t’A = tA + ∆tA
• ∆eA = getInputPrice (∆tA, tA, eA)
• e’A = eA – ∆eA
• e’B = eB – ∆eA
• ∆eB = getInputPrice (∆eA, eB, tB)
• t’B = tB – ∆tB

tokenToTokenExact

De la même façon, lLa fonction tokenToTokenExact reçoit en entrée ∆tB avec tB > ∆tB > 0 et met à jour l’état de [(eA, tA, lA), (eB, tB, lB)] vers [(e’A, t’A, lA), (e’B, t’B, lB)] où :

• t’B = tB – ∆tB
• ∆eB = getOutputPrice (∆tB, eB, tB)
• e’B = eB + ∆eB
• e’A = eA – ∆eB
• ∆tA = getOutputPrice (∆eB, tA, eA)
• t’A = tA + ∆tA

Nous en avons fini avec les principales fonctions régissant un AMM à produit constant.

Implémentation des AMM à fonction constante

Nous avons décrit ici l’approche formelle pour concevoir un AMM à fonction constante ou Constant Function Automated Market Maker pour des jetons ERC-20 sur Ethereum. Cette formalisation fut proposée par Yi Zhang, Xiaohong Chen et Daejun Park le 24 octobre 2018. Elle le point de départ d’Uniswap, la fameuse plateforme DeFi. Elle est toujours l’un des échangeur les plus utilisés sur Ethereum. En termes de volume, les échanges décentralisés représentent plus de 10 milliards de dollars.

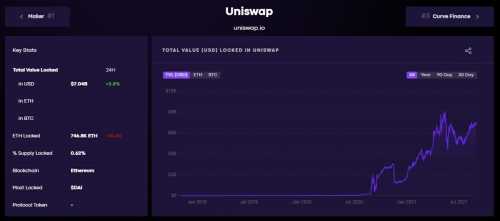
La TVL (total value locked, les fonds verrouillés) sur Uniswap – DeFi Pulse

Dans la quatrième partie de cette série, nous allons étudier Uniswap, afin d’obtenir les connaissances de base en termes d’AMM sur Ethereum, avant de nous tourner vers des modèles plus complexes.

Bibliographie

• https://uniswap.org/whitepaper.pdf
• https://angeris.github.io/papers/uniswap_analysis.pdf
• https://web.stanford.edu/~boyd/papers/pdf/cfmm.pdf
• https://cryptoeconomicsystems.pubpub.org/pub/angeris-uniswap-analysis/release/15
• https://pdfcoffee.com/uniswap-formulas-pdf-free.html

Source: journalducoin.com