Satoshi Nakamoto a-t-il programmé la mort de Bitcoin ? – Chapitre I : « Cryptographie »

30 Février 2023 – l’hiver cryptographique continue de nous épuiser par son immobilité qui paraît presque immuable. Le bitcoin continue d’errer autour des 18 000 dollars, et même les mauvaises nouvelles semblent s’arrêter de pleuvoir. Et pourtant, cette nuit-là, nos inspecteurs de données on-chain remarquent un événement que l’on attendait plus. Satoshi Nakamoto a transféré son million de bitcoins vers un autre wallet. Arrêt de mort pour Bitcoin ?

Table des matières

• Ultime scénario apocalyptique ou retour de l’enfant prodigue ?
• La signature éléctronique
  • Une authentification sécurisée
  • Les cinq composantes d’une signature sécurisée
• Les deux grands types de cryptographies
  • La cryptographie symétrique
  • L’échange de clé Diffie-Hellman et la cryptographie asymétrique

Ultime scénario apocalyptique ou retour de l’enfant prodigue ?

C’est un scénario largement discuté et débattu dans la sphère crypto. Que se passerait-il si l’on constatait un mouvement sur le wallet de Satoshi Nakamoto ?

On peut aisément imaginer le vent de panique que cette découverte accompagnerait. Certains songeraient à un message caché de son créateur pour annoncer que son invention à échoué. D’autres rationaliseraient la situation en s’auto-persuadant que bouger n’est pas vendre.

Et si la réalité était tout autre ? Et si ce magot d’environ 20 milliards de dollars à l’heure actuelle avait une fonction bien précise pour la sécurité même de Bitcoin ? Ce sujet sera la finalité d‘une série d’articles dans laquelle je vais vous partager l’histoire de la cryptographie. Comment celle-ci pourrait être bouleversée si, un jour, un des problèmes mathématiques du millénaire, venait à être résolu ?

Une bonne raison d’enfin comprendre, de manière vulgarisée, tous les rouages et fondements de la cryptographie au cœur de Bitcoin. Mieux vaut tard que jamais !

La signature éléctronique

Une authentification sécurisée

Avant même de parler de chaîne de block, la signature électronique est la première brique fondamentale de notre chiffromonnaie adorée. Une des composantes élémentaires de ses mécanismes cryptographiques. Un registre décentralisé de signature électronique en chaîne, qui permet l’échange d’un bien numérique par sa capacité à garder une trace de toutes les transactions effectuées. Voilà ce qu’est Bitcoin. Mais pourquoi sont-elles nécessaires ? 

Prenons comme exemple votre connexion à Facebook. Que se passerait-il si votre requête de connexion incluait votre mot de passe et identifiant en clair ? Un hacker pourrait intervenir lors de l’envoi de vos données au serveur, se faire passer pour Facebook auprès de ce dernier et les subtiliser. Même un chiffrement ne semble pas suffisant. Car ce pirate pourrait directement transmettre les identifiants chiffrés pour se connecter en votre nom.

Alors comment être sûr que vous communiquez bien avec Facebook ? C’est ici qu’intervient la nécessité d’une signature électronique, nécessaire à toute sorte d’authentification sécurisée sur le web. Que cela soit pour signer un document, ou vous connecter à votre réseau social préféré. Une authentification, parfois sans même avoir à révéler votre mot de passe ou votre clé privée. Mais comment ça marche ?

Les cinq composantes d’une signature sécurisée

Avant de répondre à cette question, attardons-nous sur les propriétés auxquelles une signature doit satisfaire afin de permettre votre authentification à travers l’exemple de nos signatures manuscrites : 

• Authenticité : la signature doit permettre de retrouver l’identité ou le pseudonyme du signataire. Pas très évident lorsque l’on regarde les gribouillis qui nous servent à signer nos chèques bancaires. 

• Infalsifiabilité : la signature doit prouver que vous seul êtes en mesure de la fournir et qu’elle ne puisse venir d’un usurpateur. Raté pour les signatures manuelles de nos parents, copiées avec succès dans nos carnets de correspondance lors de nos jeunes années de collégien. 

• Non réutilisabilité : la signature nécessite d’être unique et associée à chaque document signé. Peut-être la seule propriété à laquelle la signature manuscrite réponde avec assez de robustesse. 

• Inaltérabilité : lorsqu’un document est signé, celui-ci doit devenir inaltérable afin d’éviter toute modification que vous n’auriez pas approuvée. C’est pourquoi nous évitons de signer un chèque en blanc. Vous ne pourrez pas contester la somme écrite par la suite. 

• Irrévocabilité : enfin, la signature doit être irrévocable. Si elle répond à toutes les propriétés ci-dessus, le signataire est forcément l’auteur de celle-ci et ne doit pouvoir le nier. Ce qui peut poser rapidement des soucis dès lors qu’une signature manuscrite ou un document papier ne sont pas immuables.

La sécurité des signatures manuscrites est donc très imparfaite. En revanche, ces propriétés sont impérativement nécessaires pour des protocoles tels que Bitcoin. 

Pour revenir à mon exemple de Facebook, afin de permettre votre connexion de manière sécurisée, la plateforme doit s’authentifier auprès du serveur afin d’assurer que ce n’est pas un hacker qui tente d’usurper votre identité. Pour ce faire, un protocole de cryptographie asymétrique est utilisé, exactement comme lorsque vous signez des transactions sur la blockchain. Une fois authentifié, Facebook et le serveur s’échangeront des données par cryptographie symétrique, car plus simple et moins gourmande en ressource.

Le fonctionnement même de la signature électronique est intrinsèquement lié au protocole cryptographique choisi.

Les deux grands types de cryptographies

La cryptographie symétrique

Il existe deux grands types de cryptographie. La cryptographie symétrique, où vous et votre interlocuteur possédez une unique clé pour chiffrer et déchiffrer vos échanges. Et la cryptographie asymétrique où vous possédez chacun deux clés, une publique et une privée. 

Pour vous expliquer le fonctionnement d’une cryptographie symétrique, prenons un exemple simple :

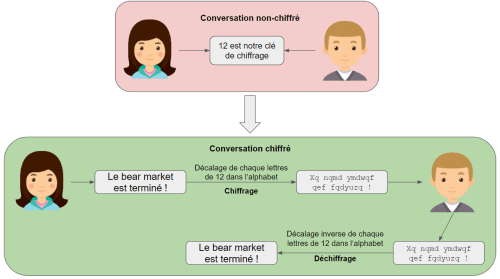
Échange d’un message secret entre Alice et Bob via un protocole de cryptographie symétrique.

Pour communiquer secrètement, Alice et Bob se mettent d’accord sur un nombre, au hasard, 12. Afin de s’envoyer un message, ils vont le chiffrer en décalant chaque lettre de leurs messages dans l’alphabet de 12 rangs. La lettre A deviendra M, la lettre B deviendra N, etc. Lorsqu’ils reçoivent un message, ils n’ont plus qu’à décaler à nouveau toutes les lettres du message dans le sens inverse pour retrouver sa signification originelle. Pas très robustes, vous en conviendrez. Mais d’autres systèmes sont imaginables. Par exemple une suite mathématique qui changerait la clé de chiffrages à chaque lettre du message.

Mais la cryptographie symétrique présente une faille. Pour pouvoir parler secrètement, Alice et Bob doivent s’accorder au préalable sur la clé de chiffrage à utiliser. Mais cet accord n’est pas chiffré et ne pourra être parfaitement secret. Il paraît donc impossible de parler secrètement sans avoir jamais parlé de manière non-secrète au préalable. Jusqu’à l’invention de l’échange de clé Diffie-Hellman qui aboutira à l’avènement de la cryptographie asymétrique.

>> Vous préférez garder vos cryptos à l’abri ? Choisissez un portefeuille Ledger (lien commercial) <<

L’échange de clé Diffie-Hellman et la cryptographie asymétrique

Ce mécanisme a été pensé pour la première fois par les cryptographes Whitfield Diffie et Martin Hellman en 1976. Il permet à deux interlocuteurs n’ayant jamais communiqué auparavant, d’échanger de manière secrète une clé de chiffrage qui servira lors de leurs futures conversations.

Ce système se base sur l’utilisation de ce que l’on appelle une fonction mathématique à sens unique. Elle agit de sorte à ce que le résultat de cette fonction appliqué à un nombre soit facilement calculable. À contrario, le chemin inverse, c’est-à-dire retrouver le nombre initial en partant du résultat, est un calcul très complexe et impossible dans un temps humainement raisonnable. Cette sécurité calculatoire est appelée l’hypothèse décisionnelle de Diffie-Hellman. Même si la fonction de chiffrage devenait publique, aucun souci à se faire, le message resterait indéchiffrable. 

Reprenons nos deux interlocuteurs Alice et Bob :

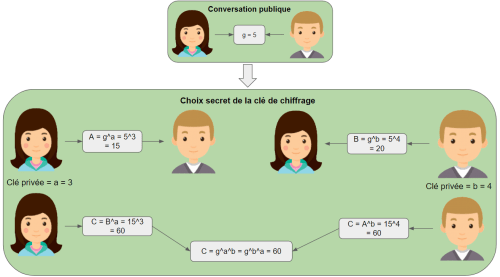
Interactions entre Alice et Bob dans un échange de clé Diffie-Hellman.

Alice et Bob vont choisir de manière non-secrète un nombre qui servira de clé publique, appelons le g et disposent chacun d’une clé privée, respectivement, a et b. Afin de se mettre en accord sur une clé de chiffrement symétrique pour leurs futures conversations, nommé C, ils vont réaliser les calculs suivants :

• Alice réalise le calcul A = g^a et envoie le résultat A à Bob.
• Bob réalise le calcul B = g^b et envoie le résultat B à Alice.
• Alice reçoit le nombre B et réalise ensuite le calcul C = B^a = (g^b)^a.
• Bob reçoit le nombre A et réalise le calcul C = A^b = (g^a)^b.

Si vous n’avez pas oublié vos cours de maths du collège, vous aurez remarqué que les calculs g^b^a et g^a^b conduisent au même résultat ! Alice et Bob ont donc trouvé une clé secrète commune pour faire de la cryptographie symétrique sans jamais se l’échanger et sans que personne ne puisse la calculer… Tant que leur clé privée, le reste !

La fonction puissance sert de fonction à sens unique. Si une troisième personne ayant accès à l’intégralité des échanges entre Alice et Bob et connaissant les nombres g, A et B, cette dernière ne pourra retrouver les clés privées a et b ainsi que le résultat final C. 

Afin d’assurer que la réalisation de ces calculs dans le chemin inverse est impossible, a et b doivent être des nombres très grands. Pour les amoureux de cryptographie, j’ai volontairement passé sous silence la partie mathématique modulaire. Elle sert à simplifier les calculs d’Alice et de Bob (et à ce que ni l’un ni l’autre ne puissent calculer la clé privée de son camarade) pour ne noyer personne. Comprenez simplement que c’est une astuce mathématique qui permet de réaliser des puissances de nombres gigantesques très facilement. Même les plus grands calculateurs du monde n’arriveraient pas à calculer par exemple 6^3000. Si vous souhaitez comprendre plus en profondeur, je vous propose d’attendre mon prochain article ! 

L’échange de clé Diffie-Hellman apporte donc une toute nouvelle façon de voir la cryptographie. Elle permet une confidentialité de bout en bout ainsi qu’une robustesse qui dépasse de très loin ce que nos ordinateurs les plus puissants sont capables de calculer tant que les clés privées des utilisateurs sont des nombres suffisamment grands. Mais cette dernière ne remplit pas encore toutes les conditions que doit posséder une signature électronique. Nous touchons seulement la cryptographie asymétrique de Bitcoin du bout du doigt. Pour aller plus loin, nous allons nous pencher sur le chiffrement RSA pour enfin aborder le chiffrement qu’utilise le bitcoin, le chiffrement ECDSA.

Mais comment diable ces grands principes cryptographiques et la sécurité qu’ils impliquent pourraient-il bien aboutir à la « mort de Bitcoin » ? Je garde ceci pour mes prochains articles, il va falloir vous armer de patience et revenir la semaine prochaine ! 

En crypto, ne faites pas l’économie de la prudence ! Ainsi, pour conserver vos avoirs cryptographiques à l’abri, la meilleure solution est encore un wallet hardware personnel. Chez Ledger, il y en a pour tous les profils et toutes les cryptos. N’attendez pas pour mettre vos capitaux en sécurité (lien commercial) !

Source: journalducoin.com