Satoshi Nakamoto a-t-il programmé la mort de Bitcoin ? – Chapitre III : « ECDSA et Hash »

Alors que la panique est déjà à son paroxysme, la société de mining Core Scientific lance une ultime alerte. Les blocks de Bitcoin sont validés depuis une heure par une unique entité nommée mystérieusement « Satoshi, it’s time », avec une cadence de plus de 2 770 blocs par minute. Les médias s’enflamment, « Bitcoin est mort », lit-on dans la presse spécialisée, malheureusement, pas de « Vive Bitcoin » pour compléter l’adage.

Les plus grands chefs d’Etat du monde prennent la parole pour démentir une quelconque implication de leur part. Google et la Chine ayant apporté les preuves qu’ils n’étaient pas en mesure de cracker par « brute force » des clés privées via leurs ordinateurs quantiques, c’est au tour de la Corée du Nord et du groupe Lazarus de subir le poids des accusations. En réaction aux événements, Wall Street plonge de 30 % à l’ouverture. Nous vivions la pire séance de l’histoire, les Big Tech réalisant des pertes en centaines de milliards de dollars.

Table des matières

Signature électronique à courbe elliptique
- Construction graphique de la clé publique
- Construction graphique si k est un nombre pair
- Construction graphique si k est un nombre impair
- Réversibilité de la construction graphique
La fonction de hashage
Le bouclier énergétique du réseau Bitcoin
- Le problème mathématique que résolvent les mineurs
- Analogie Auroral et bouclier énergétique

Dans les deux précédents articles de cette série [1]|[2], nous avons fait un gros détour sur les bases de la cryptographie moderne. Notamment autour de la signature électronique. Et si nous embrayions sur notre cher Bitcoin, et le hashage cryptographique ?

Signature électronique à courbe elliptique

Construction graphique de la clé publique

Contrairement au protocole RSA qui utilise des nombres premiers aléatoire, le chiffrement ECDSA (Elliptic Curve Digital Signature Algorithm) utilise lui des courbes elliptiques pour générer les paires de clés publiques et privées. Là, je vous vois trembler. Mais ne vous en faites pas, je ne rentrerai pas dans les mathématiques très complexes de l’ECDSA comme pour le protocole RSA qui restait “relativement” vulgarisable.

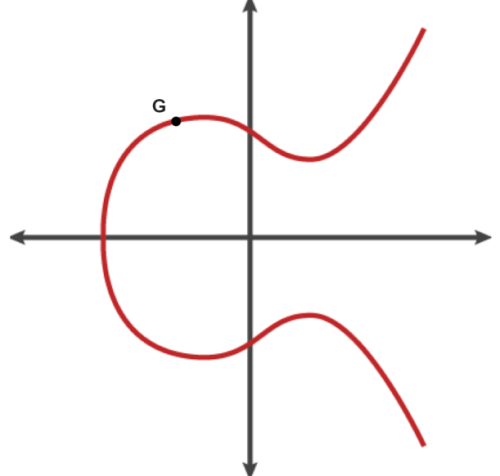
Courbe elliptique utilisée pour la génération des clés privée et publique

Ce protocole de chiffrement se base donc sur ces courbes assez singulières. Heureusement, nous allons pouvoir outrepasser ses équations cubiques et autres joyeusetés mathématiques en construisant une paire de clés de manière graphique. Pour ce faire, nous aurons besoin d’un générateur, représenté par le point G sur la courbe. Votre clé privée, appelons-le k, sera un nombre aléatoire très grand de 256 bits. Comment calcule-t-on votre clé publique à partir de votre clé privée ? Mathématiquement, c’est très simple, le résultat suivant déterminera votre clé publique P :

P = k*G

Cela vous parait trop simple ? Ne posez pas de question, c’est dû aux mathématiques assez particulières des courbes elliptiques !

Construction graphique si k est un nombre pair

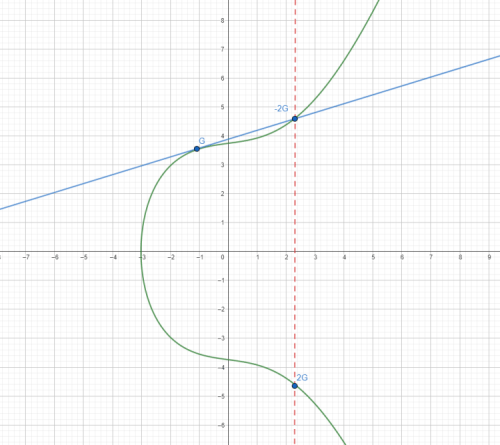
Construction graphique de la clé publique

Afin de construire votre clé publique, nous réaliserons des additions successives du point G. Imaginons que votre clé privée soit le nombre 2. Pour trouver votre clé publique P, nous calculerons le résultat de 2*G soit G+G, ce qui se traduit comme ceci :

Le nombre 2G est le point symétrique, par l’axe des abscisses, de l’intersection de la courbe elliptique et de la tangente passant par G.

Si votre clé privée est 4, nous répéterons la procédure en partant du point 2G. Le résultat 2G + 2G = 4G est le symétrique du point coupé par la tangente passant par 2G.

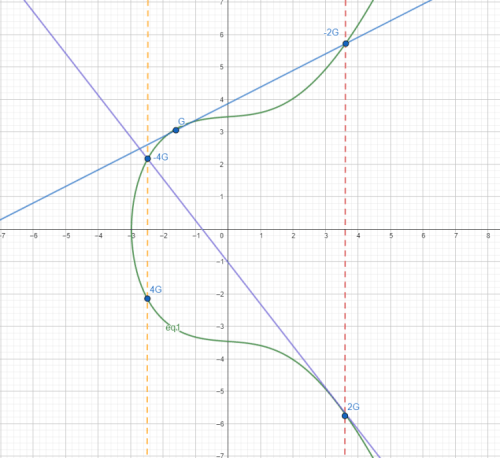
Généralisation à tout nombre k pair

Et ainsi de suite pour tous les puissances de 2. Pour construire les autres nombres pairs, il sera nécessaire de faire des additions avec les nombres précédemment construits. Par exemple 4G + 2G pour k = 6.

>> Vous préférez garder vos cryptos à l’abri ? Choisissez un portefeuille Ledger (lien commercial) <<

Construction graphique si k est un nombre impair

Si votre clé privée est un nombre impair, par exemple 3, nous tracerons la droite passant par 2G et G. Si nous généralisons à tout nombre impair :

P = (k-1)G + G

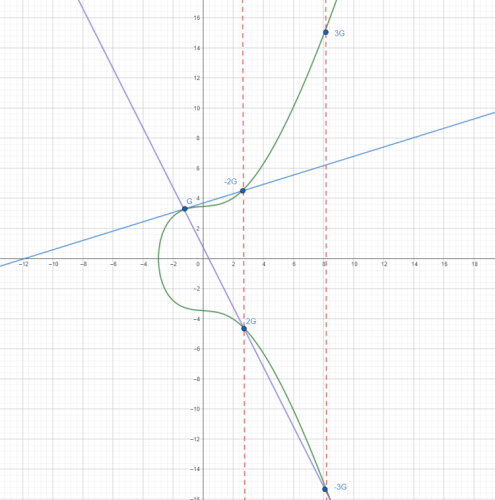
Généralisation à tout nombre k impair

Réversibilité de la construction graphique

Comme vous le voyez, il est plutôt simple de construire graphiquement votre clé publique pour des petits nombres. De même, un ordinateur réalisera sans soucis ce calcul avec des nombres gigantesques. Il suffira de répéter l’opération autant de fois que nécessaire.

En revanche, pensez-vous que cette construction est réversible ? Si je vous donnais un point au hasard sur la courbe, vous n’auriez aucun indice sur l’étape suivante. Les possibilités étant infinies.

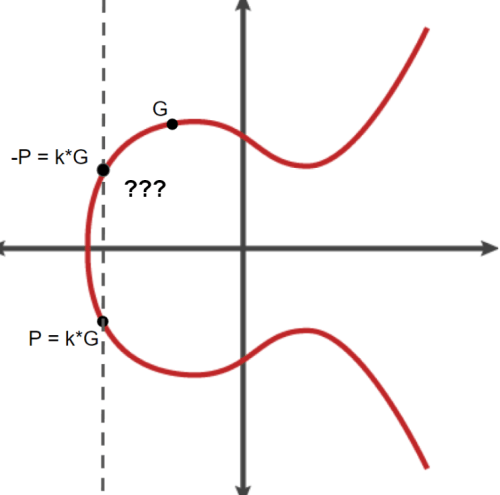
Par où commenceriez-vous si vous deviez retrouver le nombre k ?

C’est tout simplement impossible graphiquement. Et partir de G afin de générer toutes les possibilités serait comme chercher un atome dans une soupe d’univers primordial. Sachant un nombre k de 256 bits, le nombre de clés privées possible est plus grand que le nombre d’atomes dans l’univers. C’est ce qui en fait la robustesse de la génération de clés Bitcoin.

2^256 possibilités de clés privées. Pensez vous être capable de comprendre la taille de ce nombre ?
(Spoiler : vous ne pouvez pas, mais je vais quand même essayer de vous le représenter)

Imaginez 4 milliards de galaxies comportant chacune 4 milliards de versions de la planète Terre où chacun de ses 8 milliards d’humains posséderait la puissance totale de tous les mineurs de bitcoin de la planète. Si cette armada de puissance de calcul testerait toutes les possibilités de clés privées pendant 37 fois l’âge de l’univers, il n’aurait qu’une chance sur 400 millions de trouver la clé de Satoshi Nakamoto.

Pour ce faire, il serait nécessaire du consommer cinq fois plus d’énergie que celle libéré au cours de la totalité de la durée de vie de toutes les étoiles de l’univers.

Je vous laisse méditer ces quelques phrases…

Laissons donc tomber le « brute force ». Mathématiquement, la complexité d’inverser la génération de clés, vient lui aussi du problème du calcul du logarithme discret. Nous ne savons pas l’inverser efficacement sans un temps qui ne sera pas déraisonnablement et inimaginablement long.

La fonction de hashage

Le hashage est loin d’être une fonctionnalité réservée au Bitcoin. Il a de nombreuses applications, notamment dans la vérification de données lorsque l’on réalise des copies de documents très volumineux.

Par nature, le hashage associe à une donnée de taille arbitraire, une image à taille fixe qui sert d’empreinte numérique. C’est-à-dire que si vous hashez deux chaînes de caractère de longueur totalement différentes, vous trouverez deux hash de longueur identique. Le hashage est une compression irréversible d’une donnée. Dans la cryptographie, elle doit répondre à plusieurs propriétés.

Déterministe : appliquer deux fois la même fonction de hashage à une même donnée dois conduire au même résultat.
Effet avalanche : le résultat de la fonction de hashage pour deux données extrêmement proche doit conduire à des résultats très différents.
Rapide à calculer : il doit être facile à recalculer pour vérifier rapidement le hash d’une donnée. Je vous laisse deviner la quatrième propriété ?
À sens unique : afin de renforcer la propriété suivante et permettre le cryptage irréversible des données.
Résistant aux collisions : permettant l’impossibilité de construire ou modifier des données qui puissent conduire au même hash qu’une autre donnée. Il doit même être immensément improbable de pouvoir trouver deux données conduisant au même hash. Le meilleur moyen de répondre à cette problématique est d’allonger la longueur des hash. Par exemple, SHA-256 possèdent des hash de 256 bits, soit 1 chance sur 2^128, que deux données conduisent au même hash (si vous trouvez ce nombre plus faible qu’attendu et étonnant que la réponse ne soit pas 2^256, je vous renvoie au paradoxe des anniversaires).

Pour ce qui est de SHA-256, il est prouvé qu’elle est déterministe. En revanche, pour toutes les autres propriétés, nous ne savons pas ! La validation mathématique de ces propriétés est encore un problème ouvert qui n’a jusqu’à présent pas pu être démontré. Et ceci est valable pour toutes les autres fonctions de hashage. Ceci serait-il la clé de voûte de ma série d’articles ?

En rédigeant le plan de ce long sujet, j’avais l’intention de vous expliquer comment œuvrait la fonction de hashage de Bitcoin. Mais vraiment, ni vous, ni moi, n’avons envie de subir ça. Surtout dans un format écrit. Si ça vous intéresse, je vous renvoie à cette vidéo qui résume très bien son fonctionnement.

Retenez seulement que la fonction SHA-256 est une suite de différentes fonctions simples à effectuer pour un ordinateur tel que des additions modulaires, de fonction non-linéaire et opération bit à bit afin de compresser une information en une chaîne de caractère de 256 bits.

Mais soit, ce qui nous intéresse vraiment, c’est l’application de cette fonction dans la preuve de travail du réseau Bitcoin.

Le bouclier énergétique du réseau Bitcoin

Le problème mathématique que résolvent les mineurs

Les mineurs sont mis en compétition afin de calculer le hash d’un block qui est constitué de plusieurs éléments :

Le “merke root hash” ou hash en arbre de merkel de toutes les transactions contenue dans le block,
Le hash du block précédent,
L’horodatage du block,
La version du block (version 4 depuis 2015),
Le seuil cible (j’y reviens juste après),
Un nombre aléatoire ajouté au block par les mineurs que l’on nomme « nonce ».

Le défi pour les mineurs, est d’implémenter un nombre aléatoire, le « nonce », dans les données du block dont le hash résultant validera les conditions données par le seuil cible. Le seuil cible est une valeur de hash à ne pas excéder, déterminé en fonction de la difficulté de minage. Les mineurs vont répéter plusieurs millions de milliards de fois ces essais aléatoires. Lorsqu’un mineur trouve un « nonce » qui valide un hash plus faible que le hash de seuil, ce qui en théorie doit toujours prendre environ 10 min. Il est autorisé à s’auto-attribuer les nouveaux bitcoins minés à la clé !

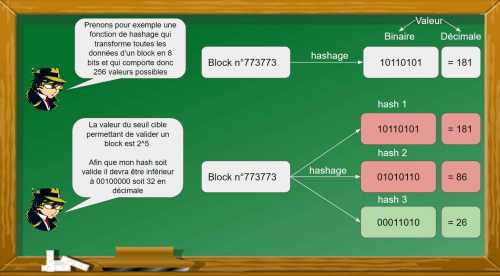
Choix d’un « nonce » aléatoire validant un hash inférieur au seuil cible

Si vous avez bien compris ce que représentait un hash, c’est ici que vous froncez les sourcils. Je vous ai dit auparavant qu’un hash faisait toujours la même taille, et maintenant il doit être plus petit qu’un certain nombre ? Le seuil cible représente une valeur, à ne pas confondre avec la taille du hash. Un hash avec la fonction SHA-256 est toujours composé de 256 bit. Pour que sa valeur soit inférieure à 2^184, qui est la valeur de seuil actuelle, celui-ci devra comporter une chaîne d’au moins soixante-douze « 0 » en début de hash.

Plus il y a de mineurs en compétitions, plus le hashrate (le nombre total de hash par seconde de l’ensemble du réseau) sera élevé et plus l’ensemble des mineurs auront de chance de trouver rapidement un hash valide. C’est pourquoi cette valeur seuil s’ajuste. En 2018, par exemple, ce nombre était au alentour de 2^200. Signe que la difficulté était significativement plus faible qu’aujourd’hui, le seuil cible étant plus grand. Pour vous visualiser la difficulté du calcul, en moyenne, une fonction de hashage avec un « nonce » aléatoire conduit à des résultats de l’ordre de 2^252.

Analogie Auroral et bouclier énergétique

Le minage n’est rien de plus qu’un casino géant où des milliers de mineurs, pour avoir le droit de jouer, doivent acheter une machine à sous et payer sa facture électrique. Le premier joueur à aligner soixante-douze « 0 » d’affilée sur les 256 rouleaux que compte sa machine, gagne 6,25 bitcoin! Lorsque des nouveaux joueurs arrivent ou ceux déjà présents achètent d’autres machines à sous, afin de ne pas ruiner le casino et ne permettre qu’un gagnant toutes les dix minutes, les chances de gagner cette loterie géante doivent diminuer. Ce n’est plus soixante-douze « 0 » d’affilé qui doivent apparaître sur les machines, mais soixante-treize.

Enfin, en apportant une notion d’aléatoire par l’ajout d’un « nonce » par les mineurs, l’algorithme de minage permet d’apporter de la complexité à la validation d’un block. Il devient donc nécessaire de réaliser le hashage en boucle afin de trouver un hash plus faible que la valeur de seuil. C’est ce travail énergétique qui fait la robustesse de la blockchain. Pour pouvoir modifier un block déjà forgé, il faudrait être en mesure de refaire ce travail afin de contaminer le réseau avec un registre invalide.

Seulement la vérification de la validité du registre prend infiniment moins de temps que celui nécessaire pour recommencer la preuve de travail. Ce mécanisme assure que le registre que vous possédez n’a pas été trafiqué. Cela coûterait beaucoup trop cher et demanderait un temps trop long afin de devancer le registre admis par le consensus en construisant une chaine parallèle plus longue que celle de ce dernier.

Lors de ces trois premiers articles, nous avons passé en revue quelques principes généraux de la cryptographie et appliqué au Bitcoin. Mais je sens la question trotter dans vos têtes depuis un petit moment, pourquoi tous ces détours ? Vous aurez la réponse dans mon prochain et dernier article de la série. Nous y verrons, malgré toutes les preuves apportées sur la robustesse de ces protocoles et leur irréversibilité, comment il pourrait s’effondrer, du jour au lendemain.

Zone d’exclusion, 30 Février 2023 16h00 — Le blizzard gronde sur la ville de Pripyat où un homme est venu s’installer là où personne n’oserait venir le chercher. Réfugié en autarcie dans une ancienne bâtisse forestière abandonnée à une dizaine de kilomètres de la centrale nucléaire de Tchernobyl, il s’y était terré afin de consacrer sa vie à sa dernière tâche. Pour seuls compagnons, des dizaines de tableaux noirs bardés de formules mathématiques incompréhensibles qu’il remplit inlassablement depuis une dizaine d’années maintenant.

Depuis qu’il est devenu incontrôlable et a atteint des centaines de milliards de dollars de valorisation, c’est devenu maladif chez lui. Pour s’auto-persuader que cette formidable invention ne ferait pas plus de mal à l’humanité que de bien, il dédiait le peu de temps qui lui restait à répondre à une question. Espérant qu’il saurait prouver la négative. En haut de son tableau noir, on peut lire : « P = NP ? ». Après une nouvelle nuit de travail acharné, il sent que la réponse n’est plus très loin, mais la fatigue l’emporte. Il remonte à l’étage, se verse une lampée de vodka artisanale pour se réchauffer, et allume l’ordinateur qu’il a pu récemment connecter à Internet via l’apport de Starlink par Elon Musk à la faveur de la guerre en Ukraine passée non loin de son sanctuaire.

C’est à ce moment-là qu’il apprend la nouvelle. Le verre se fracasse sur le sol. « Quelqu’un m’a devancé » marmonne-t-il, complètement désorienté. « Tout ceci n’a plus de sens maintenant, je n’ai plus à me cacher, je dois prendre la parole ». L’homme reprend ses esprits et se tourne vers le mur où sont affichés les derniers messages échangés avec ses amis cypherpunk l’ayant aidé dans son formidable chantier. Il décroche un papier, y dépose son regard une dernière fois, puis le jette dans l’âtre réchauffant la pièce. « Désolé mon défunt ami, j’ai échoué ». L’homme attrape sa veste et sort affronter le blizzard afin de rejoindre la civilisation qu’il a si longtemps quittée.

Le feu crépite, une bûche craque et fait virevolter le message que l’homme avait jeté, finissant de se consumer dans les airs, marquant la fin d’une ère.

« Merci pour ta contribution à une société plus juste, tu es l’homme le plus brillant que j’eus le plaisir de connaître. Merci, Satoshi. »

Hal Finney”

En crypto, ne faites pas l’économie de la prudence ! Ainsi, pour conserver vos avoirs cryptographiques à l’abri, la meilleure solution est encore un wallet hardware personnel. Chez Ledger, il y en a pour tous les profils et toutes les cryptos. N’attendez pas pour mettre vos capitaux en sécurité (lien commercial) !

Source: journalducoin.com